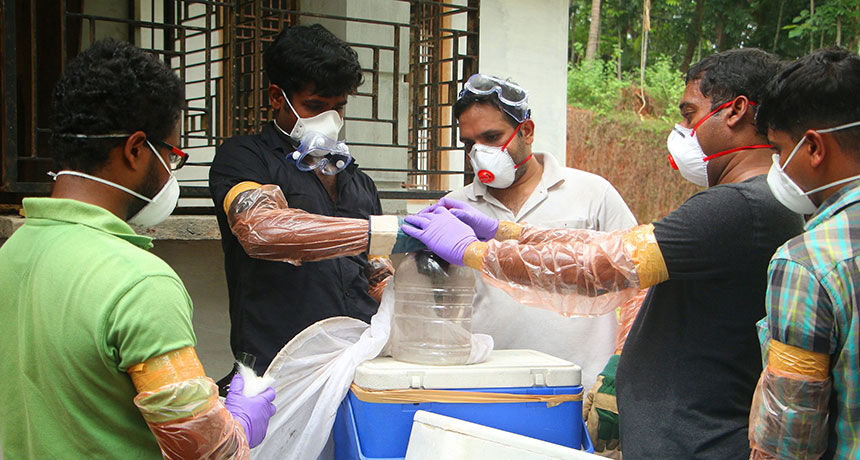
Bull sharks and bottlenose dolphins are moving north as the ocean warms

Far from their usual tropical waters, some 200 bottlenose dolphins and about 70 false killer whales have been spotted off the western coast of Canada’s Vancouver Island. Over on the Atlantic coast, bull sharks have turned a North Carolina estuary into a nursery — a sight more familiar in Florida, until now.
Two new studies highlight the unusual northern sightings of these three ocean predators.“Alone, these sightings could be seen as accidental, or vagrancies,” says marine ecologist Luke Halpin of Halpin Wildlife Research in Vancouver and part of the team tracking the dolphins sighting. “But we’re seeing a lot of warm-water species ranging into historically cold North Pacific waters.” Those include dwarf sperm whales (Kogia sima), pygmy sperm whales (Kogia breviceps) and short-finned pilot whales (Globicephala macrorhynchus) documented by other researchers.
The results suggest that these marine species will increasingly migrate outside of their typical range as climate change increases ocean temperatures, researchers say. In just the last century, average sea temperatures have risen every decade by 0.07 degrees Celsius, though temperature changes can vary widely by location.
The eastern North Pacific Ocean had experienced a three-year period of warming from 2013 to 2016, and by July 2017, water temperatures about 180 kilometers offshore of Vancouver Island hit 16.5° C. That’s smack in the middle of the range that common bottlenose dolphins (Tursiops truncatus) prefer and at the low end for false killer whales (Pseudorca crassidens).
Typically, bottlenose dolphins aren’t found in offshore waters above Eureka, Calif., and false killer whales don’t venture north of Pismo Beach, Calif. But during a routine seabird and marine mammal survey, Halpin spotted a large herd of the marine mammals off the boat’s stern. He watched for 40 minutes as the dolphins and false killer whales leaped through the water and paused to spyhop, popping their heads up vertically out of the water. At one point, some came within 400 meters of the boat. It was the first time either species had been seen in noncoastal waters of the Canadian Pacific, the researchers report online April 20 in Marine Biodiversity Records.
A similar trend is being seen in the Atlantic Ocean, with baby bull sharks appearing in increasing numbers every year since 2011 in Pamlico Sound in North Carolina, another research team reports online April 16 in Scientific Reports. Previously, the northernmost nursery for bull sharks (Carcharhinus leucas) had been Florida’s Indian River Lagoon.
But since 2008, water temperatures in early summer, when bull sharks give birth to live young, have exceeded 25° Celsius more than 60 percent of the time in the North Carolina estuary. Salinity also has slowly increased in the sound over the last few decades, from a range of 4.5 to 18.3 parts per thousand in 1971 to 9 to 17.4 parts per thousand since 2011. Young bull sharks are found only in salinities higher than 9 parts per thousand.
Changing conditions in the sound have created “the comfort zone that bull sharks will reproduce in,” says marine ecologist Charles Bangley of the Smithsonian Environmental Research Center in Edgewater, Md., lead author on the shark study.
Migration by these three top-level ocean predators could have consequences for predator-prey relationships, says marine ecologist Rebecca Selden at Rutgers University in New Brunswick, N.J., who was not involved in either of the studies. Dolphins and sharks eat a wide range of prey, so as they move into new areas, prey species there may encounter these larger predators for the first time. That could impact populations of prey species, which in turn could “cause some big ecosystem effects,” she says.